Answer:
Therefore the smallest parameters is (6,6) and a dimension of 24 inches
Explanation:
From the question we are told that
area of dimension is
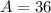
Generally the perimeter of rectangle is given as
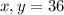
Given by
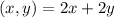
Mathematical solving for perimeter of rectangle
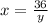
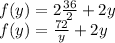
Generally in finding minimum perimeter
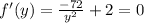
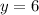
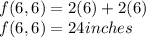
Therefore the smallest parameters is (6,6) and a dimension of 24 inches