Question

Find the smallest perimeter and the dimensions for a rectangle with an area of 36 in squared.

Answer 1

Therefore the smallest parameters is (6,6) and a dimension of 24 inches

Explanation:

From the question we are told that

area of dimension is
`A=36`

Generally the perimeter of rectangle is given as

`x,y=36`

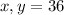
Given by

`(x,y)=2x+2y`

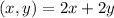
Mathematical solving for perimeter of rectangle

`x=(36)/(y)`

`f(y)= 2(36)/(2) +2y\\f(y)= (72)/(y) +2y`

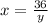
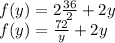
Generally in finding minimum perimeter

`f'(y)=(-72)/(y^2) +2=0\\`

`y=6`

`f(6,6)=2(6)+2(6) \\f(6,6)=24 inches`

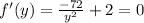
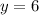
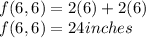
Therefore the smallest parameters is (6,6) and a dimension of 24 inches