Question

A potter's wheel moves uniformly from rest to an angular speed of 0.17 rev/s in 32.0 s.

a. Find its angular acceleration in radians per second per second.
b. Would doubling the angular acceleration during the given period have doubled final angular speed?

Answer 1

a) α = 0.0334 rad / s² , b) w = 2.14 rad/s see that the angular velocity doubles.

Step-by-step explanation:

This is a magular kinematics exercise

Let's reduce the magnitudes to the SI system

w = 0.17 rev /s (2π rad / 1rev) = 1.07 rad / s

a) as part of rest its initial velocity is zero w or = 0

w = w₀ + α t

α =
`(\omega -\omega_(o) )/(t)`

α =
`(1.07-0)/(32)`

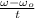
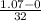
α = 0.0334 rad / s²

b) If we double the angular relation what will be the final velocity

w = w₀ + (2α) t

w = 0 + 2 0.0334 32

w = 2.14 rad/s

We see that the angular velocity doubles.