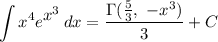Answer:
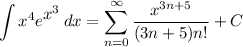
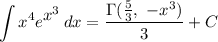
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Integration
- Integrals
- [Indefinite Integrals] Integration Constant C
Integration Property [Multiplied Constant]:
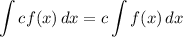
U-Substitution
Sequences
Series
Taylor Polynomials and Approximations
- MacLaurin Polynomials
- Taylor Polynomials
Power Series
- Power Series of Elementary Functions
- Taylor Series:
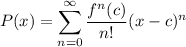
Integration of Power Series:
-
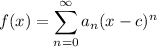
-
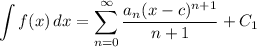
Multivariable Calculus
Gamma Functions
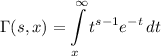
- Incomplete Gamma Functions
Explanation:
*Note:
If we are talking single-variable calculus, then we would have to write this integral as a power series.
- You can derive the power series for eˣ using Taylor Polynomials (not shown here)
If we are talking multi-variable calculus, then we could integrate this and get an "actual" value.
Single-variable Calculus
We are given the integral:
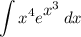
We know that the power series for
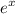 is:
is:
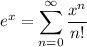
To find the power series for
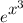 , substitute in x = x³:
, substitute in x = x³:
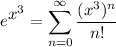
Simplify it, we have:
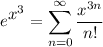
Rewrite the original function:
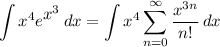
Rewrite the integrand by including the x⁴ in the power series:
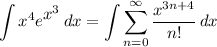
Integrating the power series, we have:
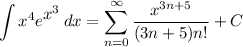
Multivariable Calculus
Let's set our variables for u-substitution:
u = x⁵ → du = 5x⁴ dx
Use u-substitution on the integral to obtain:
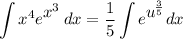
We see that the integral is an incomplete gamma function:
![\displaystyle \int {x^4e^\big{x^3}} \, dx = (1)/(5) \bigg[ \frac{5 \Gamma ((5)/(3), \ -u^\big{(3)/(5)})}{3} \bigg] + C](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dccj7b98f9zpi8391jugs1ifwy9ugta9n5.png)
Simplifying it, we have:

Back-substituting u will give us the final result: