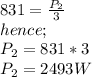Question

Three identical resistors are connected in series. when a certain potential difference is applied across the combination, the total power dissipated is 277 w. what power would be dissipated if the three resistors were connected in parallel across the same potential difference?

Answer 1

2493W

Step-by-step explanation:

The relationship between the power P consumed by a resistor R and the potential difference V across the it is given by;

`P=(V^2)/(R)..............(1)`

According to the problem stated, the potential difference V is constant.

If V is kept constant, then we can write the following;

`PR=V^2..............(2)`

Equation (2) implies that we can write the following as long as V is kept constant;

`P_1R_1=P_2R_2=...=P_nR_n...........(3)`

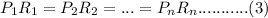
We can simply write equation (3) as;

`P_1R_1=P_2R_2..............(4)`

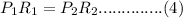
From the problem stated,
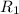`R_1` is a series combination of three identical resistors while
`R_2` is their parallel combination. Let the value of each resistor be R, hence;

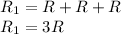`R_1=R+R+R\\R_1=3R` (series combination)

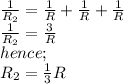`(1)/(R_2)=(1)/(R)+(1)/(R)+(1)/(R)\\(1)/(R_2)=(3)/(R)\\hence;\\R_2=(1)/(3)R` (parallel combination)

Given;

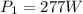`P_1=277W` for the series combination, are supposed to find
`P_2` for the parallel combination. Hence we make the necessary substitutions into equation (4) as follows;

`277*3R=P_2*(1)/(3)R\\831R=P_2*(1)/(3)R`

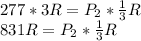
R cancels out from both sides and we get the following,

`831=(P_2)/(3)\\hence;\\P_2=831*3\\P_2=2493W`

Answer 2

Answer;

= 2493 W

Explanation;

The total resistance of 3 resistors in series = R + R + R = 3 * R

The total resistance of 3 resistors in parallel = 1 ÷ (1/R + 1/R + 1/R) = ⅓ R

At the same voltage, V, the total current in the series circuit will be

= V ÷ (3 * R)

= ⅓ * V/R.

At the same voltage, V, the total current in the parallel circuit will be;

= V ÷ (⅓ R)

= 3 * V/R

At the same voltage, the parallel circuit will have 9 times the amperage of the series circuit.

Power = Volts * amps

Power of series circuit = V * ⅓ * V/R = ⅓ * V^2/R

Power of parallel circuit = 3 * V^2/R

But, power of series is 277 W

1/3 (V²/R) = 277

(V²/R) = 277 × 3

Power in parallel = 3 V²/R

= 277 × 3 × 3

= 2493 W