Hello!
The answer is: B)
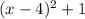
Why?
Since from the graph we can only see the position of the vertex (4,1), let's find the vertex of the chosen option (B).
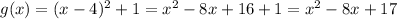
Where:
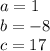
Finding the vertex:
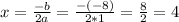
So, x-coordinate of the vertex is 4,
Susbtituting x into the function, we can find the y-coordinate

So, y-coordinate of the vertex is 1
Hence,
The Vertex is located at (4,1)
If the vertex is located at (4,1), then the chosen option is correct.
Have a nice day!