Question

What are the vertex and x-intercepts of the graph of y=x^2-2x-24

Answer 1

Explanation:

What are the vertex and x-intercepts of the graph of y=x^2-2x-24

Direction: Opens Up

Vertex:

(1,−25)

Focus:

(1,−994)

Axis of Symmetry:

x=1

Directrix:

y=−101/4

x y

−1 −21

0 −24

1 −25

2 −24

3 −21

Answer 2

Vertex : (1,-25) ; x intercepts : (6,0)&(-4,0)

Explanation:

`y=x^(2)-2x-24`

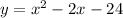
adding 25 on both sides

`y+25=x^(2)-2x-24+25`

`y+25=x^(2)-2x+1`

`y+25=x^(2)-2*1*1*x+1^(2)`

`y+25=(x-1)^(2)`

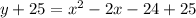
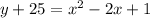
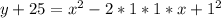
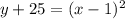
let us convert the above equation in the standard form

let y+25=Y

x-1=X

`X^(2)=4*(1)/(4)*Y`

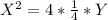
vertex of above equation is (0,0)

replacing them into original form is x-1=0 , x=1

y+25=0 ; y=-25

Hence the vertex is (1,-25)

Part 2 :

In order to find the x intercepts , we put y=0 and solve for x

`0+25=(x-1)^(2)`

`25=(x-1)^(2)`

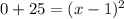
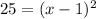
taking square roots on both sides we get

±5=x-1

solving get x=±5+1 ; x=5+1=6 ; x=-5+1=-4

Hence y intercepts are (-4,0) & (6,0)