Answer:
Vertex : (1,-25) ; x intercepts : (6,0)&(-4,0)
Explanation:
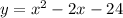
adding 25 on both sides

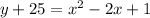
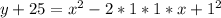
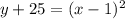
let us convert the above equation in the standard form
let y+25=Y
x-1=X
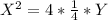
vertex of above equation is (0,0)
replacing them into original form is x-1=0 , x=1
y+25=0 ; y=-25
Hence the vertex is (1,-25)
Part 2 :
In order to find the x intercepts , we put y=0 and solve for x
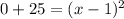

taking square roots on both sides we get
±5=x-1
solving get x=±5+1 ; x=5+1=6 ; x=-5+1=-4
Hence y intercepts are (-4,0) & (6,0)