Question

Please help me find the inverse

Answer 1

`f^(-1)(x)` is supposed to be a function such that

`f^(-1)(f(x))=x`

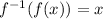
In this case, we need

`f^(-1)(\sqrt[3]{x-2})=x`

To recover
`x` from
`\sqrt[3]{x-2}`, we would first need to raise
`\sqrt[3]{x-2}` to the third power:

`(\sqrt[3]{x-2})^3=x-2`

Then add 2:

`(x-2)+2=x`

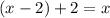
To recap, we carried out

`f^(-1)(\sqrt[3]{x-2})=(\sqrt[3]{x-2})^3+2=x`

which implies that the inverse function is

`f^(-1)(x)=x^3+2`

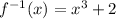
To verify: we should also have that
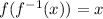`f(f^(-1)(x))=x`. We get

`f(x^3+2)=\sqrt[3]{(x^3+2)-2}=\sqrt[3]{x^3}=x`