Answer:
1.

2.

3.
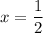
4.

5.
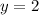
6. There are no holes for this function.
7. There are no oblique asymptotes.
Explanation:
Consider the function
 The denominator of the fraction includes the expression
The denominator of the fraction includes the expression
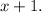 Since the denominator cannot be equal to 0, then
Since the denominator cannot be equal to 0, then

Thus, the range is

and line
 is a vertical asymptote.
is a vertical asymptote.
The roots of the function are:

When

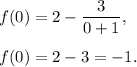
Point (0,-1) is y-intercept.
The line
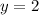 is a horizontal asymptote.
is a horizontal asymptote.
There are no holes for this function.
There are no oblique asymptotes.