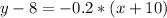Answer:
The answer is
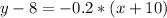
Explanation:
In order to determine the correct option, we have to know about point-slope form.
The point-slope form is the way that we can create linear functions from a point and a slope. The formula is:
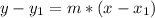
Where:
 : Coordinates of the point.
: Coordinates of the point.
m: Slope
Also we can get the slope from two points. The formula is:

 : Coordinates of the first point.
: Coordinates of the first point.
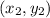 : Coordinates of the second point.
: Coordinates of the second point.
So first we determine the slope:
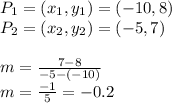
Finally, the correct option is: