Question

`f(x) = (x-5)/(2x^(2)-5x-3 )`

Domain:
V.A:
Roots:
Y-int:
H.A:
Holes:
O.A:

Also, draw on the graph.

Answer 1

Domain:All real numbers except x≠3 and x≠ -1/2,V.A= x=3 , x= -1/2.root=5,y-int= 5/3.H.A=0 , no hole , no O.A.

Explanation:

We have given the function:

`(x-5)/(2x^(2)-5x-3 )`

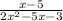
So, first we simplify the equation we get,

`(x-5)/((x-3)(2x+1))`

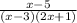
We have to find the domain :

Domain is the value of x for which the function is defined.

For this, denominator must not be equal to zero.

(x-3)(2x+1) ≠ 0

(x-3)≠0 , (2x+1)≠0

x≠3 , x≠ -1/2

So, the domain is all real numbers except x≠3 and x≠ -1/2.

For vertical asymptotes, denominator is equal to zero.

(x-3)(2x+1) = 0

x=3 , x= -1/2 are vertical asymptotes.

Nominator is equal to zero for roots:

x-5 = 0

x= 5 is the root.

Put x = 0 for y-intercept:

y = 0-5/(0-3)(2(0)+1)

y = 5/3 is the y-intercept.

Horizontal asymptote is :

`\lim_(x \to \infty) (x-5)/(2x^(2)-5x-3)=0`

Horizontal asymptote is y = 0.

The function has no hole because it is reducible.

It has no oblique asymptote because it is proper function.

Graph is attached.

Answer 2

i) The given function is

`f(x)=(x-5)/(2x^2-5x-3)`

The factored form is

`f(x)=(x-5)/((x-3)(2x+1))`

The domain are the values of x for which the function is defined.

`(x-3)(2x+1)\\e 0`

`(x-3)\\e0,(2x+1)\\e 0`

`x\\e3,x\\e-(1)/(2)`

ii) To find the vertical asymptotes, equate the denominator to zero.

`(x-3)(2x+1)=0`

`(x-3)=\\e0,(2x+1)=0`

`x=3,x=-(1)/(2)`

iii) To find the roots, equate the numerator to zero.

`x-5=0`

The root is
`x=5`

iv) To find the y-intercept, put
`x=0` into the function.

`f(0)=(0-5)/((0-3)(2(0)+1))`

`f(0)=(-5)/((-3)(1))`

`f(0)=(5)/(3)`

The y-intercept is
`(5)/(3)`

v) The horizontal asymptote is given by;

`lim_(x\to \infty)(x-5)/(2x^2-5x-3)=0`

The horizontal asymptote is
`y=0`

vi) The function is not reducible. There are no holes.

vii) The given function is a proper rational function.

Proper rational functions do not have oblique asymptotes.