Question

`f(x) = ((2x+1)(x-5))/((x-5)(x+4)^(2) )`

Domain:
V.A:
Roots:
Y-int:
H.A:
Holes:
O.A:

Also, draw on the graph attached.

Answer 1

i) The given function is

`f(x)=((2x+1)(x-5))/((x-5)(x+4)^2)`

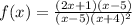
The domain is

`(x-5)(x+4)^2\\e 0`

`(x-5)\\e0,(x+4)^2\\e 0`

`x\\e5,x\\e -4`

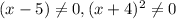
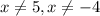
ii) For vertical asymptotes, we simplify the function to get;

`f(x)=((2x+1))/((x+4)^2)`

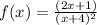
The vertical asymptote occurs at

`(x+4)^2=0`

`x=-4`

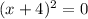
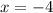
iii) The roots are the x-intercepts of the reduced fraction.

Equate the numerator of the reduced fraction to zero.

`2x+1=0`

`2x=-1`

`x=-(1)/(2)`

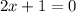
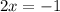
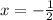
iv) To find the y-intercept, we substitute
`x=0` into the reduced fraction.

`f(0)=((2(0)+1))/((0+4)^2)`

`f(0)=((1))/((4)^2)`

`f(0)=(1)/(16)`

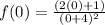
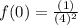
v) The horizontal asymptote is given by;

`lim_(x\to \infty)((2x+1))/((x+4)^2)=0`

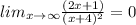
The horizontal asymptote is
`y=0`.

vi) The function has a hole at
`x-5=0`.

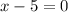Thus at
`x=5`.

This is the factor common to both the numerator and the denominator.

vii) The function is a proper rational function.

Proper rational functions do not have oblique asymptotes.