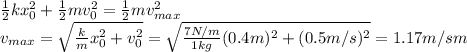Question

A 1 kg mass is attached to a spring with spring constant 7 Nt/m. What is the frequency of the simple harmonic motion? What is the periodSuppose the mass is displaced 0.4 meters from its equilibrium position and released from rest. What is the amplitude of the motionSuppose the mass is released from the equilibrium position with an initial velocity of 0.5 meters/sec. What is the amplitude of the motion? Suppose the mass is is displaced 0.4 meters from the equilibrium position and released with an initial velocity of 0.5 meters/sec. What is the amplitude of the motion? What is the maximum velocity? m/s

Answer 1

1) The frequency of the simple harmonic motion is
`f=0.42(1)/(s)`.

The period is
`T=2.37s`.

2) If the mass is displaced 0.4 m from its equilibrium position and released from rest, the amplitude of the motion is
`A=0.4m`.

3) If the mass is released from its equilibrium position with an initial velocity of 0.5 m/s, the amplitude of the motion is
`A=0.19m`.

4) If the mass is displaced 0.4 m from its equilibrium position and released with an initial velocity of 0.5 m/s, the amplitude of the motion is
`A=0.44m` and the maximum velocity is
`v_(max) =1.16(m)/(s)`.

Step-by-step explanation:

1) The simple harmonic motion frequency in a system like a mass attached to a spring is determined by the spring constant k, that indicates the stiffness of the spring, and the mass m:

`f=(w)/(2\pi) =(1)/(2\pi) \sqrt{(k)/(m)}`

where
`w=\sqrt{(k)/(m)}` is the angular frequency

we are told that
`k=7(N)/(m)` and
`m=1kg`

`f=(1)/(2\pi)\sqrt{(7N/m)/(1kg)}`

`f=(1)/(2\pi)\sqrt{7(1)/(s^(2))}`

`f=0.42(1)/(s)`

the period T is

`T=(1)/(f)`

`T=2\pi \sqrt{(m)/(k)}`

`T=2.37s`

2) The amplitude is the maximum displacement from equilibrium. If there are no dissipative forces it remains the same throughout the movement. We are told that the mass is displaced 0.4 m from its equilibrium position and released from rest. Then the amplitude of the motion is
`A=0.4m`.

3) Depending on the initial conditions we will choose sine or cosine, both periodic, for the expression of displacement as a function of time
`x(t)`. If the mass is displaced a given lenght at t=0 we use cosine. If the mass is at equilibrium position x=0 at t=0 we use sine.

We are told the mass is released from its equilibrium position x=0 at t=0 with an initial velocity of 0.5 m/s. We substitute those values in the expression of velocity that we derive from the expression of displacement as a function of time. We assume the phase to be
`\phi=0`.

`x(t)=Asin(wt-\phi)`

`(dx)/(dt)=v(t)=Awcos(wt-\phi)`

`v(t=0)=Aw=A\sqrt{(k)/(m)}`

`0.5(m)/(s) =A√(7) (1)/(s)`

`A=0.19m`

4) We are told the mass is displaced 0.4 m from its equilibrium position and released with an initial velocity of 0.5 m/s. The expressions of velocity and of displacement as a function of time are:

`x(t)=Acos(wt-\phi)`

`v(t)=-Awsin(wt-\phi)`

if we substitute t=0

`x_(0) =x(t=0)=Acos(\phi)`

`v_(0)=v(t=0)=-Awsin(\phi)`

then we use the trigonometric identities
`cos(-\phi)=cos(\phi)` and
`sin(-\phi)=-sin(\phi)`

`x_(0) ^(2)=A^(2)cos(\phi)^(2)`

`(v_(0) ^(2))/(w^(2)) =A^(2)sin(\phi)^(2)`

if we add this two expressions we get

`x_(0)^(2)+(v_(0) ^(2))/(w^(2)) =A^(2)(sin(\phi)^(2)+cos(\phi)^(2))`

we use the trigonometric identity
`(sin(\phi)^(2)+cos(\phi)^(2))=1` to get

`A=\sqrt{x_(0)^(2)+(v_(0) ^(2))/(w^(2))}`
`A=\sqrt{(0.4)^(2)m^(2)+((0.5)^(2)(m^(2))/(s^(2)))/((√(7))^(2)(1)/(s^(2)))}`

`A=\sqrt{(0.4)^(2)+((0.5)^(2))/((√(7))^(2)))m^(2)}`

`A=0.44m`

maximum velocity occurs when
`sin(wt-\phi)=-1` in the expression of
`v(t)`

`v_(max)=Aw`

`v_(max)=0.44m .√(7) (1)/(s)`

`v_(max) =1.16(m)/(s)`

Answer 2

1. 0.42 Hz

The frequency of a simple harmonic motion for a spring is given by:

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

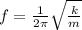
where

k = 7 N/m is the spring constant

m = 1 kg is the mass attached to the spring

Substituting these numbers into the formula, we find

`f=(1)/(2\pi)\sqrt{(7 N/m)/(1 kg)}=0.42 Hz`

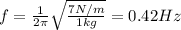
2. 2.38 s

The period of the harmonic motion is equal to the reciprocal of the frequency:

`T=(1)/(f)`

where f = 0.42 Hz is the frequency. Substituting into the formula, we find

`T=(1)/(0.42 Hz)=2.38 s`

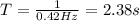
3. 0.4 m

The amplitude in a simple harmonic motion corresponds to the maximum displacement of the mass-spring system. In this case, the mass is initially displaced by 0.4 m: this means that during its oscillation later, the displacement cannot be larger than this value (otherwise energy conservation would be violated). Therefore, this represents the maximum displacement of the mass-spring system, so it corresponds to the amplitude.

4. 0.19 m

We can solve this part of the problem by using the law of conservation of energy. In fact:

- When the mass is released from equilibrium position, the compression/stretching of the spring is zero:
`x=0`, so the elastic potential energy is zero, and all the mechanical energy of the system is just equal to the kinetic energy of the mass:

`E=K=(1)/(2)mv^2`

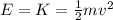
where m = 1 kg and v = 0.5 m/s is the initial velocity of the mass

- When the spring reaches the maximum compression/stretching (x=A=amplitude), the velocity of the system is zero, so the kinetic energy is zero, and all the mechanical energy is just elastic potential energy:

`E=U=(1)/(2)kA^2`

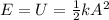
Since the total energy must be conserved, we have:

`(1)/(2)mv^2 = (1)/(2)kA^2\\A=\sqrt{(m)/(k)}v=\sqrt{(1 kg)/(7 N/m)}(0.5 m/s)=0.19 m`

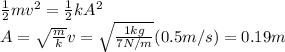
5. Amplitude of the motion: 0.44 m

We can use again the law of conservation of energy.

-
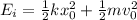`E_i = (1)/(2)kx_0^2 + (1)/(2)mv_0^2` is the initial mechanical energy of the system, with
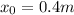`x_0=0.4 m` being the initial displacement of the mass and
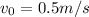`v_0=0.5 m/s` being the initial velocity

`- E_f = (1)/(2)kA^2` is the mechanical energy of the system when x=A (maximum displacement)

Equalizing the two expressions, we can solve to find A, the amplitude:

`(1)/(2)kx_0^2 + (1)/(2)mv_0^2=(1)/(2)kA^2\\A=\sqrt{x_0^2+(m)/(k)v_0^2}=\sqrt{(0.4 m)^2+(1 kg)/(7 N/m)(0.5 m/s)^2}=0.44 m`

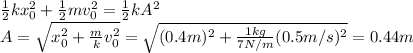
6. Maximum velocity: 1.17 m/s

We can use again the law of conservation of energy.

-
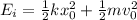`E_i = (1)/(2)kx_0^2 + (1)/(2)mv_0^2` is the initial mechanical energy of the system, with
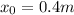`x_0=0.4 m` being the initial displacement of the mass and
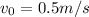`v_0=0.5 m/s` being the initial velocity

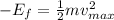`- E_f = (1)/(2)mv_(max)^2` is the mechanical energy of the system when x=0, which is when the system has maximum velocity,
`v_(max)`

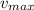
Equalizing the two expressions, we can solve to find
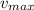`v_(max)`, the maximum velocity:

`(1)/(2)kx_0^2 + (1)/(2)mv_0^2=(1)/(2)mv_(max)^2\\v_(max)=\sqrt{(k)/(m)x_0^2+v_0^2}=\sqrt{(7 N/m)/(1 kg)(0.4 m)^2+(0.5 m/s)^2}=1.17 m/s m`