Question

`f(x) = (3(x-1)(x+1))/((x-3)(x+3))`

Domain:
V.A:
Roots:
Y-int:
H.A:
Holes:
O.A:

Also, draw on the graph attached.

Answer 1

QUESTION 1

i) The given function is

`f(x)=(3(x-1)(x+1))/((x-3)(x+3))`

The domain is

`(x-3)(x+3)\\e0`

`(x-3)\\e0,(x+3)\\e0`

`x\\e3,x\\e-3`

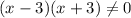
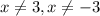
ii) To find the vertical asymptote equate the denminator to zero.

`(x-3)(x+3)\=0`

`(x-3)=0,(x+3)=0`

`x=3,x=-3`

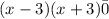
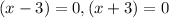
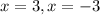
iii) To find the roots equate the numerator zero.

`3(x-1)(x+1)=0`

`3(x-1)=0,(x+1)=0`

`(x-1)=0, (x+1)=0`

`x=1, x=-1`

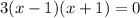
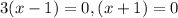
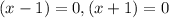
iv) To find the y-intercept substitute
`x=0` into the function;

`f(0)=(3(0-1)(0+1))/((0-3)(0+3))`

`f(0)=(-3)/((-3)(3))`

`f(0)=(1)/(3)`

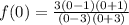
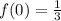
The y-intercept is
`(1)/(3)`

v) The horizontal asymptote is given by

`lim_(x\to \infty)(3(x-1)(x+1))/((x-3)(x+3))=3`

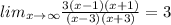
The horizontal asymptote is y=3

vi) The rational function has no common linear factor.

This rational function has no holes.

vii) This rational function is a proper function. It has no oblique asymptote.