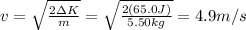Question

A 5.50 kg sled is initially at rest on a frictionless horizontal road. The sled is pulled a distance of 3.20 m by a force of 25.0 N applied to the sled at an angle of 30° to the horizontal.

(a) Find the work done by the applied force.
(b) Find the energy dissipated by friction.
(c) Find the change in the kinetic energy of the sled.
(d) Find the speed of the sled after it has traveled 3 m.

Answer 1

(a) 69.3 J

The work done by the applied force is given by:

`W=Fd cos \theta`

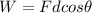
where:

F = 25.0 N is the magnitude of the applied force

d = 3.20 m is the displacement of the sled

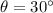`\theta=30^(\circ)` is the angle between the direction of the force and the displacement of the sled

Substituting numbers into the formula, we find

`W=(25.0 N)(3.20 m)(cos 30^(\circ))=69.3 J`

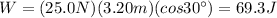
(b) 0

The problem says that the surface is frictionless: this means that no friction is acting on the sled, therefore the energy dissipated by friction must be zero.

(c) 69.3 J

According to the work-energy theorem, the work done by the applied force is equal to the change in kinetic energy of the sled:

`\Delta K = W`

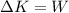
where

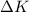`\Delta K` is the change in kinetic energy

W is the work done

Since we already calculated W in part (a):

W = 69.3 J

We therefore know that the change in kinetic energy of the sled is equal to this value:

`\Delta K=69.3 J`

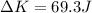
(d) 4.9 m/s

The change in kinetic energy of the sled can be rewritten as:

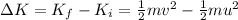`\Delta K=K_f - K_i = (1)/(2)mv^2-(1)/(2)mu^2` (1)

where

Kf is the final kinetic energy

Ki is the initial kinetic energy

m = 5.50 kg is the mass of the sled

u = 0 is the initial speed of the sled

v = ? is the final speed of the sled

We can calculate the variation of kinetic energy of the sled,
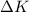`\Delta K`, after it has travelled for d=3 m. Using the work-energy theorem again, we find

`\Delta K= W = Fd cos \theta =(25.0 N)(3.0 m)(cos 30^(\circ))=65.0 J`

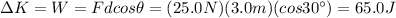
And substituting into (1) and re-arrangin the equation, we find

`v=\sqrt{(2 \Delta K)/(m)}=\sqrt{(2(65.0 J))/(5.50 kg)}=4.9 m/s`