Question

The height h (in inches) above the water of a pelican before a dive is modeled by h=-16t^2+70t+50, where t is time (in seconds)

a) When does the pelican enter the water
b)How high above the water is the pelican at time t=0 seconds

Answer 1

a) 5 seconds.

b) 50 inches.

Step-by-step explanation

The height of the pelican is modeled by,

`h(t) = - 16t^(2) + 70t + 50`

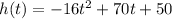
The pelican enters the when

`h(t) = 0`

`- 16t^(2) + 70t + 50 = 0`

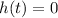
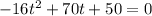
Divide through by negative 2,

`8 {t}^(2) - 35t - 25 = 0`

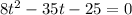
Factor to obtain

`(t - 5)(8t + 5) = 0`

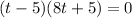
This implies that,

`t = 5 \: or \: t = - (5)/(8)`

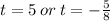
Time cannot be negative, therefore the water after 5 seconds.

B) The height of the pelican is modeled by

`h(t) = - 16t^(2) + 70t + 50`

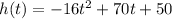
When

`t = 0`

`h(0) = - 16(0)^(2) + 70(0) + 50`

`h(0) = 50`

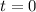
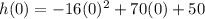
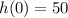
The pelican was 50 inches above the water at time t=0.