Answer:
The range is 94 ,variance is 1141.564 and standard deviation is 33.7870
Explanation:
We need to find out the range , variance and standard deviation
Given data:- 14, 94, 26, 79,50,72,99,93,60,5,88
Range is calculated as;
Range = the difference between the highest and lowest numbers
Highest = 99
Lowest = 5
Range = 99 - 5 = 94
Now to find the variance of the given data , we first need to find the mean
The mean of the data is calculate by sum of all data is divided by total number of data
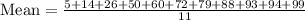
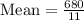
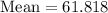
Variance is calculated by formula:

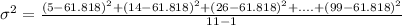
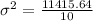
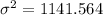
Now, we will calculate standard deviation by taking square root over variation,
Standard Deviation =
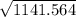
=
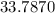
Therefore, the range is 94 ,variance is 1141.564 and standard deviation is 33.7870