Question

Below are the jersey numbers of 11 players randomly selected from a football team. Find the range, variance, and standard deviation for the given sample data. 14, 94, 26, 79,50,72,99,93,60,5,88​

Answer 1

The range is 94 ,variance is 1141.564 and standard deviation is 33.7870

Explanation:

We need to find out the range , variance and standard deviation

Given data:- 14, 94, 26, 79,50,72,99,93,60,5,88​

Range is calculated as;

Range = the difference between the highest and lowest numbers

Highest = 99

Lowest = 5

Range = 99 - 5 = 94

Now to find the variance of the given data , we first need to find the mean

The mean of the data is calculate by sum of all data is divided by total number of data

`\text{Mean}=(5+14+26+50+60+72+79+88+93+94+99)/(11)`

`\text{Mean}=(680)/(11)`

`\text{Mean}=61.818`

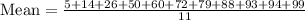
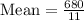
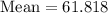
Variance is calculated by formula:

`\sigma^(2)=((x_i-mean)^(2))/(n-1)`

`\sigma^(2)=((5-61.818)^(2)+(14-61.818)^(2)+(26-61.818)^(2)+....+(99-61.818)^(2))/(11-1)`

`\sigma^(2)=(11415.64)/(10)`

`\sigma^(2)=1141.564`

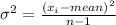
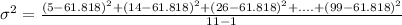
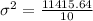
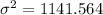
Now, we will calculate standard deviation by taking square root over variation,

Standard Deviation =
`√(1141.564)`

=
`33.7870`

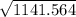
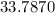
Therefore, the range is 94 ,variance is 1141.564 and standard deviation is 33.7870

Answer 2

Range =94

σ² = 1,141.564

Standard Deviation = 33.78703

Step-by-step explanation:

First off to find the range, we find the highest value and subtract it to the lowest value. In this situation the values are:

Highest = 99

Lowest = 5

Range = 99 - 5

Range = 94

Now to find the variance of the sample data set, we first need to find for the mean of the data.

The mean of the data with be the sum of all the numbers in the data set divided by the number of samples.

Mean =
`(5+14+26+50+60+72+79+88+93+94+99)/(11)`

Mean =
`(680)/(11)`

Mean =
`61.81818`

Now to find the variance we simply use the formula:

σ²
`=((x_(i)-Mean)^(2) )/(n-1)`

σ²
`=((5-61.818)^(2)+(14-61.818)^(2)+(26-61.818)^(2)+...+(99-61.818)^(2) )/(11-1)`

σ²
`=(11,415.64)/(10)`

σ²
`=1,141.564`

Now to find the standard deviation, we take the variance and get the square root of it.

Standard Deviation
`=√(1,141.564)`

Standard Deviation
`=33.78703`