Question

Tanya drives to work every day and passes two independently operated traffic lights. The probability that both lights are red is 0.55. The probability that the first light is red is 0.69. What is the probability that the second light is red, given that the first light is red?

Answer 1

0.797%

Explanation:

Step 1: Find the probability that both lights are red and that the first light is red

This is P(A ∩ B)

P(Both lights are red )=0.55

This is P(B)

P (first light is red) = 0.69

Step 2: use the formula P(A∩B)/P(B)

0.55/0.69=0.79710144

0.797%

Answer 2

`P(B|A) = 0.797`

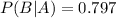
Explanation:

Call A to the event that represents a red light at the first traffic light

Then, call B the event that represents a red light at the second traffic light.

Then we know that:

P(A∩B) = 0.55

P(A) = 0.69

Then the probability that the second light is red because the first one is red is:

`P(B|A) = (P(A\ and\ B))/(P(A))`

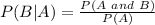
Then:

`P(B|A) = (0.55)/(0.69)\\\\P(B|A) = 0.797`

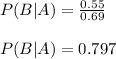
There is a 79.7% chance that the second light is in red