Answer:
Solution set of the quadratic inequality is { x : x ∈ R and x < -2 }
Explanation:
Given Quadratic inequality ,
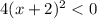
We have to find solution set of the given quadratic inequality.
consider,
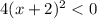
transpose 4 to RHS
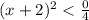
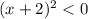
Square root both side,
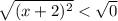
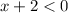
transpose 2 to RHS
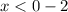
x < -2
Solution set of the quadratic inequality = { x : x ∈ R and x < -2 }
Therefore, Solution set of the quadratic inequality is { x : x ∈ R and x < -2 }