Answer:
The sphere is taller than the cube
Explanation:
we know that
The height of the cube is equal to the length side of the cube and the height of the sphere is equal to the diameter of the sphere
step 1
Find the length side of the cube
we know that
The volume of the cube is equal to
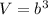
where
b is the length side of the cube
we have
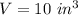
substitute and solve for b
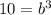
![b=\sqrt[3]{10}\ in](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ia3odf3bqe3yrot2q4lea5lqoxtw49kgyf.png)
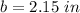
step 2
Find the diameter of the sphere
we know that
The volume of the sphere is equal to

we have
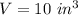
substitute and solve for r

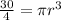
![r=\sqrt[3]{(30)/(4\pi)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z6kjvd1tysclziqi2ll8e9j9zsai5t9pg7.png)
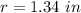
Find the diameter
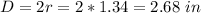
step 3
Compare
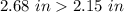
therefore
The sphere is taller than the cube