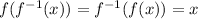Answer:
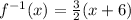
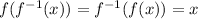
Explanation:
Given
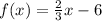
Required
Determine
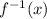
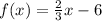
Represent f(x) as y
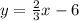
Swap the positions of x and y
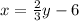
Add 6 to both sides
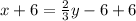
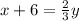
Multiply both sides by 3
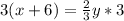
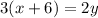
Divide both sides by 2
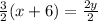
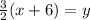
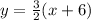
Replace y with
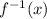
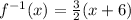
Justify the result:
First, we solve for
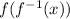
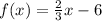
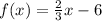 becomes
becomes
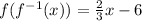
Substitute
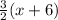 for x
for x
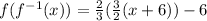
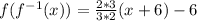
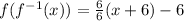
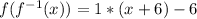
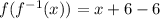
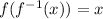
Next, we solve
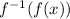
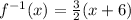
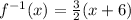 becomes
becomes
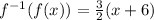
Substitute
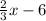 for x
for x
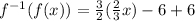
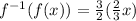
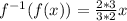
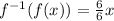
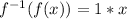
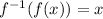
Hence: