Answer:
may experience a magnetic force, but its speed will not change.
Step-by-step explanation:
A charged particle moving in a static uniform magnetic field experiences a magnetic force (called Lorentz force) which is given by:
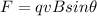
where
q is the charge
v is the speed of the particle
B is the magnetic field intensity
is the angle between the direction of the motion of the charge and the direction of the magnetic field
We can notice that when
(so, when the particle is moving parallel to the field), the magnetic force is zero, so the particle does not experience any force. This means that we can immediately exclude the following choice:
- will always experience a magnetic force, regardless of its direction of motion.
Moreover, the magnetic force acts perpendicular to the direction of motion of the particle. This means it will change the direction of motion of the particle, so we can also exclude the following option
- may experience a magnetic force, but its direction of motion will not change.
Finally, the fact that the magnetic force is perpendicular to the direction of motion of the particle also implies that the force does no work on the particle. According to the work-energy theorem (which states that the kinetic energy gained by the particle is equal to the work done on it), this implies that the particle gains no kinetic energy, so its speed does not change. This allows us to exclude also the following choice
- a magnetic force which will cause its speed to change.
Therefore, the correct option is the only one remained:
- may experience a magnetic force, but its speed will not change.