Question

CD is the perpendicular bisector of both XY and ST and CY=20.

Find CX

A.5

B.15

C.20

D.22

Answer 1

Is a 5 percent effective

Answer 2

The correct option is C.

Explanation:

It is given that CD is the perpendicular bisector of both XY and ST, and CY=20.

In triangle XCD and YCD,

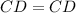`CD=CD` (Common sides)

`\angle XDC=\angle YDC=90^(\circ)` (Definition of perpendicular bisector)

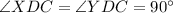`\angle XD=\angle YD` (Definition of perpendicular bisector)

By SAS postulate of congruent triangles,

`\triangle XCD=\triangle YCD`

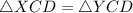
The corresponding parts of congruent triangle are congruent,

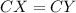`CX=CY` (CPCTC)

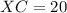`XC=20` (CY=20)

The length of CX is 20 units. Therefore the correct option is C.