Question

Find an equation in standard form for the hyperbola with vertices at (0, ±9) and foci at (0, ±11)

Answer 1

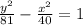`(y^(2) )/(81) -(x^(2) )/(40) }=1` is standard equation of hyperbola with vertices at (0, ±9) and foci at (0, ±11).

Explanation:

We have given the vertices at (0, ±9) and foci at (0, ±11).

Let (0,±a) = (0,±9) and (0,±c) = (0,±11)

The standard equation of parabola is:

`(y^(2) )/(a^(2) ) -(x^(2) )/(b^(2) )=1`

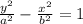
From statement, a = 9

c² = a²+b²

(11)² = (9)²+b²

121-81 = b²

40 = b²

Putting the value of a² and b² in standard equation of parabola, we have

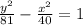`(y^(2) )/(81) -(x^(2) )/(40) }=1` which is the answer.