Answer:
Increase by a factor of four
Step-by-step explanation:
The force between the two charged particle is directly proportional to the product of charges and inversely proportional to the square of the distance between them. This law is known as Coulomb's law. Mathematically, it can be written as :
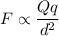
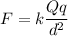
Where
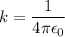
And this force divided by electric charge is equal to electric field i.e.
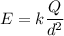
So, the electric field is inversely proportional to the distance.


E' = 4 E
When d is halved, the force field between the particles increase by a factor of four. Hence, the correct option is (c).