Answers:
(a) The kinetic energy of a body is that energy it possesses due to its movement and is defined as:
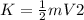 (1)
(1)
Where
 is the mass of the body and
is the mass of the body and
 its velocity.
its velocity.
In this specific case of the satellite, its kinetic energy
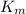 taking into account its mass
taking into account its mass
 is:
is:
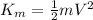 (2)
(2)
On the other hand, the velocity of a satellite describing a circular orbit is constant and defined by the following expression:
 (3)
(3)
Where
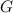 is the gravity constant,
is the gravity constant,
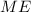 the mass of the Earth and
the mass of the Earth and
 the radius of the orbit (measured from the center of the Earth to the satellite).
the radius of the orbit (measured from the center of the Earth to the satellite).
Now, if we substitute the value of
 from equation (3) on equation (2), we will have the final expression of the kinetic energy of this satellite:
from equation (3) on equation (2), we will have the final expression of the kinetic energy of this satellite:
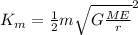 (4)
(4)
Finally:
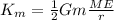 (5) >>>>This is the kinetic energy of the satellite
(5) >>>>This is the kinetic energy of the satellite
(b) According to Kepler’s 2nd Law applied in the case of a circular orbit, its Period
 is defined as:
is defined as:
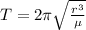 (6)
(6)
Where
 is a constant and is equal to
is a constant and is equal to
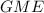 . So, this equation in these terms is written as:
. So, this equation in these terms is written as:
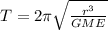 (7)
(7)
As we can see, the Period of the orbit does not depend on the mass of the satellite
 , it depends on the mass of the greater body (the Earth in this case)
, it depends on the mass of the greater body (the Earth in this case)
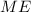 , the radius of the orbit and the gravity constant.
, the radius of the orbit and the gravity constant.
(c) The gravitational force described by the law of gravity is a central force and therefore is a conservative force. This means:
1. The work performed by a gravitational force to move a body from a position A to a position B only depends on these positions and not on the path followed to get from A to B.
2. When the path that the body follows between A and B is a closed path or cycle (as this case with a circular orbit), the gravitational work is null or zero.
This is because the gravity force that maintains an object in circular motion is a centripetal force, that is, it always acts perpendicular to the movement.
Then, in the case of the satellite orbiting the Earth in a circular orbit, its movement will always be perpendicular to the gravity force that attracts it to the planet, at each point of its path.
(d) The total Mechanical Energy
 of a body is the sum of its Kinetic Energy
of a body is the sum of its Kinetic Energy
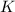 and its Potential Energy
and its Potential Energy
 :
:
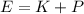 (8)
(8)
But in this specific case of the circular orbit, its kinetic energy will be expresses as calculated in the first answer (equation 5):
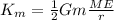 (5)
(5)
And its potential energy due to the Earth gravitational field as:
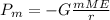 (9)
(9)
This energy is negative by definition.
So, the total mechanical energy of the orbit, also called the Orbital Energy is:
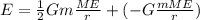 (10)
(10)
Solving equation (10) we finally have the Orbital Energy:
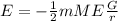 (11)
(11)
At this point, it is necessary to clarify that a satellite (or any other celestial body) orbiting another massive body, can describe one of these types of orbits depending on its Orbital Total Mechanical Energy
 :
:
-When
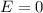 :
:
We are talking about an open orbit in which the satellite escapes from the attraction of the planet's gravitational field. The shape of its trajectory is a parabola, fulfilling the following condition:

Such is the case of some comets in the solar system.
-When
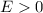 :
:
We are also talking about open orbits, which are hyperbolic, being
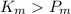
-When
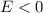 : >>>>This case
: >>>>This case
We are talking about closed orbits, that is, the satellite will always be "linked" to the gravitational field of the planet and will describe an orbit that periodically repeats with a shape determined by the relationship between its kinetic and potential energy, as follows:
-Elliptical orbit: Although
 is constant,
is constant,
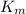 and
and
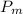 are changing along the trajectory .
are changing along the trajectory .
-Circular orbit: When at all times both the kinetic energy
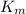 and the potential
and the potential
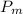 remain constant, resulting in a total mechanical energy
remain constant, resulting in a total mechanical energy
 as the one obtained in this exercise. This means that the speed is constant too and is the explanation of why this Energy has a negative sign.
as the one obtained in this exercise. This means that the speed is constant too and is the explanation of why this Energy has a negative sign.