Question

Two forces with magnitudes of 100 and 50 pounds act on an object at angles of 50° and 160°, respectively. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and in your final answer.

Answer 1

The direction and magnitude of the resultant force is 79.53° above positive x axis.

Explanation:

We are given with data as:

100 lbs at 50°

50 lbs at 160°

1st vector:

100 lbs cos(50°) = 64.3 lbs ⇒ x direction

100 lbs sin(50°) = 76.60 lbs ⇒y direction

2nd vector:

50 lbs cos(160°) = - 46.98 lbs ⇒ negative x direction

50 lbs sin(160°) = 17.10 lbs ⇒ positive y direction

Value of x:

64.3 lbs + (-46.98 lbs) = 17.32 positive x direction

Values of y:

76.60 lbs + 17.10 lbs = 93.70 positive y direction

Now

Use Pythagorean theorem to find the resultant.

a² + b² = c²

93.70² + 17.32² = c²

8779.69 + 299.98 = c²

9079.67 = c²

√9079.67 = √c²

95.29 lbs = c

So

Resultant is 95.29 lbs.

Now

Direction of the resultant vector.

Using tan we get

Θ = tan^-1 (93.7/17.32) = 79.53° above positive x axis.

Answer 2

Hello!

Since there is no additional information, we can assume that the given angles are respect to the horizontal axis (x), so

The answer is:

Magnitude: 95.14 lbs

Direction: 80° respect to the x-axis

Why?

Since there is no additional information about the given angles, we can assume that both angles are respect to the horizontal axis (x), positive direction to x-axis positive directions (right) and above x-axis.

Calculations:

100 pounds (lb) force, 50° angle:

`100lbs*cos(50)=64.28lbs\\100lbs*sin(50)=76.60lbs`

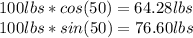
50 pounds (lb) force, 160° angle:

`50lbs*cos(160)=-46.98lbs\\50lbs*sin(160)=17.10lbs`

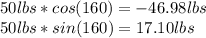
So,

For x-axis forces we have:

64.28lbs (positive direction)

-46.98lbs (negative direction)

Then,

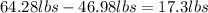`64.28lbs-46.98lbs=17.3lbs` (positive direction)

Fox y-axis forces we have:

76.60lbs (positive direction)

17.10 lbs (positive direction)

Then,

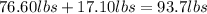`76.60lbs + 17.10 lbs =93.7lbs` (positive direction)

So, we have the two components values of the acting force:

17.3 lbs for the x-axis and 93.7 lbs for the y-axis.

Therefore,

We have to calculate the angle between both resultant force components:

Let's calll it α

So,

`\alpha=tan^(-1)((y-axisValue)/(x-axisValue))=tan^(-1)((93.7)/(17.3))\\\alpha=79.5=80`

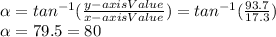
Hence, the angle between both resultant force components is 80 °, meaning that the resultant force direction is positive, above the x-axis.

Now we have to calculate the magnitude of the resultant force since the sum of both resultant force components is equal to the hypotenuse of the formed triangle, we have that:

`sin(\alpha)=(y-axisValue)/(ResultantForceMagnitude)=(93.7lbs)/(ResultantForceMagnitude)\\\\ResultantForceMagnitude=(93.7lbs)/(sin(80))=95.14lbs`

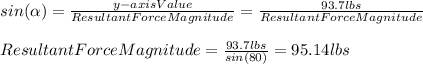
So, we have that:

• Resultant force magnitude is equal to 95.14 lbs

• Direction is 80° respect to the x-axis.

Have a nice day!