Hello!
The answer is: False, the inverse of
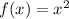 is not a function.
is not a function.
Why?
It's known that most of functions don't have an inverse function. Inverse function is known for being the result of inverting a one to one function, it means that for each y should be only one x. If the function is not a one to one function, it doesn't have an inverse that is a function
The given function is not a one to one function, let's prove it:
Let's evaluate two differentes values: 5 and -5
Evaluating 5
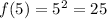
Evaluating -5
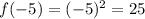
We have the same output for differents x values, so, the function is not a one to one function, meaning that its inverse is not a function.
Have a nice day!