Question

State whether f is a function

Answer 1

`((y)/(6 ))^(1/4)=f^(-1)(y)`

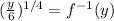
Explanation:

We have given a function.

f(x) = 6x⁴

We have to find the inverse of the given function.

Putting y=f(x) in given equation ,we have

y = 6x⁴

y/6 = x⁴

Taking 4th root to both sides of Above equation, we have

`((y)/(6))^(1/4)=x`

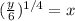
Putting x = f⁻¹(y) in above equation, we have

`((y)/(6 ))^(1/4)=f^(-1)(y)`

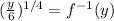
Replacing y by x , we have

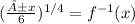`((±x)/(6 ))^(1/4)=f^(-1)(x)` which is the answer.

f⁻¹(x) is not function because it assigns each value of x to two values of y.

Choice D is correct answer.

Answer 2

`y=\pm ((x)/(6))^{(1)/(4)} \ is \ not \ a \ function`

Step by step solution:

A function
`f` from a set
`A` to a set
`B` is a relation that assigns to each element
`x` in the set
`A` exactly one element
`y` in the set
`B`. The set
`A` is the domain (also called the set of inputs) of the function and the set
`B` contains the range (also called the set of outputs). On the other hand, a function has an inverse function if and only if passes the Horizontal Line Test for Inverse Functions. This test tells us that a function
`f` has an inverse function if and only if there is no any horizontal line that intersects the graph of
`f` at more than one point. So the function is called one-to-one. The graph of
`f` is shown below. As you can see, this function does not pass the Horizontal Line Test, therefore the inverse is not a function. However, let's find
`f^-{1}(x)`:

`f(x)=6x^4 \\ \\ Substitute \ f(x) \ by \ y \\ \\ y=6x^4 \\ \\ Interchange \ x \ and \ y: \\ \\ x=6y^4 \\ \\ Solve \ for \ y: \\ \\ y^4=(x)/(6) \\ \\ Solving \\ \\y=\pm \sqrt[4]{(x)/(6)} \\ \\ \boxed{y=\pm \left((x)/(6)\right)^{(1)/(4)}}`

and this is not a function because there are elements in the set of inputs that match with two elements in the set of outputs.