Answer:
The linear function is given by:

Explanation:
It is given that the rate of change of the linear function is equal to the average rate of change of function f on the interval [-1, 1].
The slope(m) or average rate of change of the linear function will be:
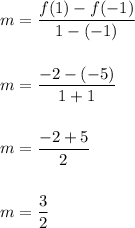
and the linear function pass through (1,-2)
We know that the equation of a line with given slope m and passing through point (a,b) is given by:
Here (a,b)=(1,-2)
and
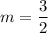
Hence, the equation of linear function is:
