We can represent the segment parametrically:

When t=0 we get P=J, when t=1 we get P=K. So when P is between J and K,
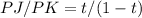
We want the point P so that
PJ/PL=2/3
That's
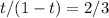
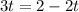
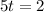
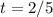
That means 2/5ths along the way from J to K, which we could have gotten immediately as 2/(2+3).

We're only after the y coordinate,
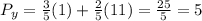
Answer: 5