Question

A man stands on the roof of a building of height 13.0m and throws a rock with a velocity of magnitude 33.0m/s at an angle of 25.3(degree) above the horizontal. You can ignore air resistance. (A)Calculate the maximum height above the roof reached by the rock. (B)Calculate the magnitude of the velocity of the rock just before it strikes the ground.(C)Calculate the horizontal distance from the base of the building to the point where the rock strikes the ground.

Answer 1

To calculate the maximum height reached by the rock, we need to analyze the vertical motion of the rock. The initial vertical velocity can be found by multiplying the initial velocity by the sine of the launch angle. In this case, the initial vertical velocity would be 33.0 m/s * sin(25.3°).

Step-by-step explanation:

To calculate the maximum height reached by the rock, we need to analyze the vertical motion of the rock. The initial vertical velocity can be found by multiplying the initial velocity by the sine of the launch angle. In this case, the initial vertical velocity would be 33.0 m/s * sin(25.3°). The time it takes for the rock to reach its maximum height can be found using the equation Vf = Vo + at, where Vf is the final vertical velocity (which is 0 at the maximum height), Vo is the initial vertical velocity, a is the acceleration due to gravity (-9.8 m/s^2), and t is the time. Using this equation, we can calculate the time it takes for the rock to reach its maximum height. The maximum height can then be calculated using the equation d = Vit + (1/2)at^2, where d is the displacement, Vi is the initial vertical velocity, a is the acceleration due to gravity, and t is the time. Lastly, to calculate the magnitude of the velocity of the rock just before it strikes the ground, we can use the equation Vf = sqrt(Vi^2 + 2ad), where Vf is the final velocity (which is unknown), Vi is the initial velocity (which remains constant), a is the acceleration due to gravity, and d is the displacement (which is the height of the building). Plugging in the known values, we can solve for the final velocity of the rock. Finally, to calculate the horizontal distance from the base of the building to the point where the rock strikes the ground, we can use the equation d = Vt, where d is the displacement, V is the horizontal component of the initial velocity, and t is the time it takes for the rock to hit the ground. We can plug in the known values to calculate the horizontal distance.

Answer 2

(a) 23.1 m

The vertical velocity of the rock at time t is given by:

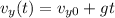`v_y(t) = v_(y0) + gt` (1)

where

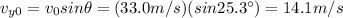`v_(y0) = v_0 sin \theta = (33.0 m/s)(sin 25.3^(\circ))=14.1 m/s` is the initial vertical velocity of the rock

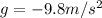`g=-9.8 m/s^2` is the acceleration due to gravity (negative because it is downward)

t is the time

At the point of maximum height, the vertical velocity is zero:

`v_y(t)=0`

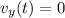
Using this information in eq.(1), we find the time it takes for the rock to reach the maximum height:

`v_(y0) + gt=0\\t=-(v_(y0))/(g)=-(14.1 m/s)/(-9.8 m/s^2)=1.44 s`

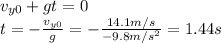
And now we can calculate the vertical position of the rock after t=1.44 s by using the equation:

`y(t)=y_0 + v_(0y)t + (1)/(2)gt^2=13.0 m+(14.1 m/s)(1.44 s)+(1)/(2)(-9.8 m/s^2)(1.44 s)^2=23.1 m`

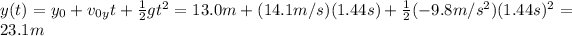
(2) 36.7 m/s

For this part, we have to calculate the time t at which the rock reaches the ground, which means y(t)=0. So:

`y(t)=0=y_0 + v_(y0)t + (1)/(2)gt^2\\0=13.0 + 14.1t - 4.9t^2`

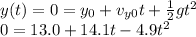
which has two solutions:

t = -0.73 s --> negative, we discard it

t = 3.61 s --> this is our solution

So now we can calculate the vertical velocity of the rock when it reaches the ground:

`v_y(t)=v_(y0) + gt = 14.1 m/s+(-9.8 m/s^2)(3.61 s)=-21.4 m/s`

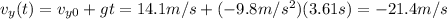
The horizontal velocity has not changed, since the motion along the horizontal direction is uniform, so it is

`v_x(t)=v_(x0)=(33.0 m/s)(cos 25.3^(\circ))=29.8 m/s`

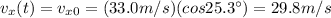
So, the magnitude of the velocity when the rock hits the ground is

`v=√(v_x^2+v_y^2)=√((-21.4 m/s)^2+(29.8 m/s)^2)=36.7 m/s`

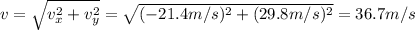
(3) 107.6 m

The horizontal distance travelled by the rock is given by:

`d=v_x t`

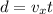
where

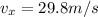`v_x = 29.8 m/s` is the horizontal velocity, which is constant

`t=3.61 s` is the time it takes for the rock to reach the ground

Substituting, we find

`d=(29.8 m/s)(3.61 s)=107.6 m`