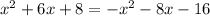Question

asked Oct 21, 2020 82.7k views

2 Answers

Rich Waters · Answer 1 · 2020-10-27T05:41:47+0000

Answer:

The equation which solves the graph of system of equation is:

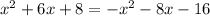
x^2+6x+8=-x^2-8x-16

(-4,0),(-3,-1) and (-2,0)

Let the equation of parabola be:

y=ax^2+bx+c

Now, when we take the point (-4,0) we have:

16a-4b+c=0----------(1)

when we take the point (-3,-1) we have:

9a-3b+c=-1---------(2)

and when we take the point (-2,0) we have:

4a-2b+c=0-----------(3)

on subtracting equation (3) from equation (1) we have:

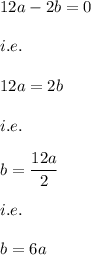
$12a-2b=0\\\\i.e.\\\\12a=2b\\\\i.e.\\\\b=(12a)/(2)\\\\i.e.\\\\b=6a$

and on putting the value of b in equation (3) we have:

$4a-2(6a)+c=0\\\\i.e.\\\\4a-12a+c=0\\\\i.e.\\\\c=8a$

Now, on putting the value of b and c in terms of a in equation (2) we have:

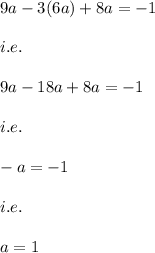
$9a-3(6a)+8a=-1\\\\i.e.\\\\9a-18a+8a=-1\\\\i.e.\\\\-a=-1\\\\i.e.\\\\a=1$

Hence,

$b=6\\\\and\\\\c=8$

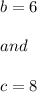
Hence, the equation of blue parabola is:

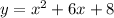
y=x^2+6x+8

(-4,0) , (-3,-1) and (-5,-1)

Hence, the three equations are:

$16a-4b+c=0----------(1)\\\\9a-3b+c=-1----------(2)\\\\25a-5b+c=-1-----------(3)$

on solving the three equations we have:

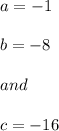
$a=-1\\\\b=-8\\\\and\\\\c=-16$

Hence, we have the equation of the red parabola as:

y=-x^2-8x-16

Hence, the equation of the graph that need to be solved is:

x^2+6x+8=-x^2-8x-16