Answer:
Eccentricity = 5/6
Type of conic section; Ellipse
Directrix; x = -11/5
Explanation:
The first step would be to write the polar equation of the conic section in standard form by multiplying the numerator and denominator by 1/6;
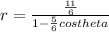
The polar equation of the conic section is now in standard form;
The eccentricity is given by the coefficient of cos theta in which case this would be the value 5/6. Therefore, the eccentricity of this conic section is 5/6.
The eccentricity is clearly between 0 and 1, implying that the conic section is an Ellipse.
Since the conic section is in standard form, the numerator is the product of eccentricity and the value of the directrix, that is;
e*d = 11/6
5/6*d = 11/6
d = 11/5
Since the denominator has a minus sign then the ellipse opens towards the right and thus the equation of its directrix is;
x = -11/5