Answer:
eccentricity; e = 1/7
k = 12
Conic section; Ellipse
Explanation:
The first step would be to write the polar equation of the conic section in standard form by multiplying the numerator and denominator by 1/7;
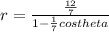
The polar equation of the conic section is now in standard form;
The eccentricity is given by the coefficient of cos theta in which case this would be the value 1/7. Therefore, the eccentricity of this conic section is 1/7.
The eccentricity is clearly between 0 and 1, implying that the conic section is an Ellipse.
The value in the numerator gives the value of k; k = 12