The exponential function is D. The exponential function is growing faster, because it grows by a factor that is multiplied by the previous y-value instead of being added like the linear function.
What is an exponential function
An exponential function is a mathematical function written as
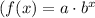 , where a represents the initial value, b is the constant base
, where a represents the initial value, b is the constant base
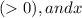 is the variable exponent.
is the variable exponent.
Their graphs display distinct curves, illustrating steep increase or decrease, and they find applications in finance, population growth, radioactive decay, and other scientific and economic phenomena.
The linear function grows by a * b
exponential grows by aˣ
Option D is correct