The root of -5 with multiplicity 3 implies that the polynomial is a multiple of
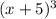
Similarly, the two other roots imply that the polynomial is a multiply of
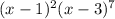
So, the minimal polynomial which satisfies your requests on the roots is
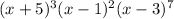
which would be a polynomial of degree 12. This polynomial would be:
- positive in
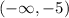
- negative in
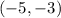
- positive in
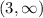
Since we want a negative leading term, the signs will be opposite: your polynomial is
- negative in
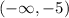
- positive in
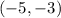
- negative in
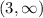
So, the only true statement is the last one.