Question

Tanya runs a catering business. Based on her records, her weekly profit can be approximated by the function LaTeX: f\left(x\right)=2x^2-44x-150 f ( x ) = 2 x 2 − 44 x − 150 , where LaTeX: x x is the number of meals she caters. If LaTeX: f(x) f ( x ) is negative, it means that the business has lost money. What is the number of meals that Tanya needs to cater in order to break-even?

Answer 1

The function

`2x^2-44x-150`

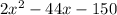
is a parabola concave up, whose solutions are

`2x^2-44x-150=0 \iff x^2-22x-75=0`

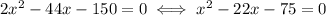
from here, you can use the quadratic formula

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a)`

to find that the solutions of the parabola are
`-3,\ 25`

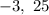
So, the parabola is positive if
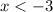`x<-3` (which wouldn't make sense in our case) or
`x<25`

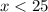
So, if Tanya caters 25 meals she breaks even, and starting with the 26th meal she will begin to profit.