Answer:
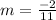 is the slope through the points.
is the slope through the points.
Explanation:
We have given two points:
(-22,3) and (11,-3)
We have to find the slope through (-22,3) and (11,-3).
As we know that
slope = m =
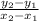
Where (x₁,y₁) = (-22,3) , (x₂,y₂) = (11,-3)
Put this values in slope equation we get,

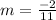
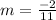 is the slope through the points.
is the slope through the points.