Question

Find the ratio of the lengths of the two mathematical pendulums, if the ratio of periods is 1.5​

Answer 1

The ratio of lengths of the two mathematical pendulums is 9:4.

Step-by-step explanation:

It is given that,

The ratio of periods of two pendulums is 1.5

Let the lengths be L₁ and L₂.

The time period of a simple pendulum is given by :

`T=2\pi \sqrt{(l)/(g)}`

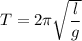
or

`T^2=4\pi^2(l)/(g)\\\\l=(T^2g)/(4\pi^2)`

Where

l is length of the pendulum

`l\propto T^2`

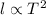
or

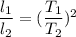`(l_1)/(l_2)=((T_1)/(T_2))^2` ....(1)

ATQ,

`(T_1)/(T_2)=1.5`

Put in equation (1)

`(l_1)/(l_2)=(1.5)^2\\\\=(9)/(4)`

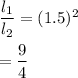
So, the ratio of lengths of the two mathematical pendulums is 9:4.