Question

Ed is planning daily walking workouts on the same distance of 12 km in the morning and in the evening. Usually he is walking at constant rate, however he planned his rate to be 1 km/h more in the morning than in the evening. Given he is willing to spend 5 hours and 24 minutes daily on these workouts, what should his morning rate be, in km/h?

Answer 1

Ed's morning rate should be 5 km/h.

Explanation:

Morning: 12/x+1↔time, x+1=speed

Evening:12/x↔time, x=speed

total:5.4 hours

12/x+1+12/x=5.4

x=-5/9, 4

x≠-5/9

x=4, x+1=5

Answer 2

Given is :

Let the rate of walking in the evening be = x km/h

As Ed wants to walk at a rate if 1 km/h more in the morning, then rate in morning becomes = x+1 km/h

So, distance is 12 km, speed is x+1 km/h

`time=(distance)/(speed)`

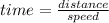
Total time is = 5 h 24 m or convert it into hours, it becomes
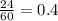`(24)/(60)=0.4` = 5.4 hours

Time in morning becomes =
`(12)/(x+1)`

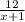
Time in evening becomes =
`(12)/(x)`

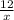
So equation becomes=
`(12)/(x+1)+(12)/(x)=5.4`

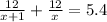
Solving this quadratic equation, we get, x= -5/9 or x=4

As X cannot be negative so neglect -5/9.

Solving by using x=4, we get rate as x= 4+1 =5 km/h

Hence, rate in the morning is 5 km/h.