(a) identify the unknown quantities and introduce variables to represent them
Answer:
Distance traveled by Amelia upstream is 12 km. Let us call it x.
So that x = 12 km
Distance traveled downstream is unknown. But by reading and understanding the question, one can tell that the distance covered on trip downstream must be the same as distance traveled while going upstream.
Let us call it y.
So that y = x = 12 km
y = 12 km
Speed of Amelia while swimming = s
Speed of the current in the river = c
(b) write equations which express the information given in the statement of the problem
Answer:
s - c = 2 ------eq-1
s + c = 6 ------eq-2
Explanation:
Speed of Amelia's swimming is same then why is the time taken while going upstream different than while going downstream?
It is because the resistance of current in the river is in the downward direction. It explains why Amelia takes more time to go upstairs and much less to come back.
Using Speed = Distance traveled/Time
While going upstream:
Amelia is going against the current, hence the direction for Amelia and river's current is opposite. We get the equation:
s - c = 12/6 = 2------eq-1 where t = 6 hours
While going downstream:
Amelia is going with the current, hence the direction for Amelia and river's current is same. We get the equation:
s + c = 12/2 = 6------eq-2 where t = 2 hours
(c) solve the equations and give the answer
Answer:
speed of the current in the river = c = 4 km/h
Explanation:
To find = c?
We will use the two equations:
s - c = 2 ------eq-1
s + c = 6 ------eq-2
From eq-1 :
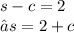
putting s = 2+c in eq-2:
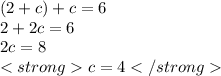
Hence; the speed of the current of the river is 4 km/h.