Question

A gas occupies 0.105 L at 105 K. At what Celsius temperature will its volume be 0.140 L? Assume that pressure remains constant. It would be great if you could show work!

Answer 1

This problem can be solved using the Combined Gas Law. The formula for it is

`(P_(1) V_(1) )/(T_(1) ) = (P_(2) V_(2) )/(T_(2) )`

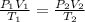
Let's go ahead and plug in the known values. Since pressure remains the same, it does not matter what value we plug in, so let's assume 1 atm for both sides.

`((1 atm) (0.105 L))/((105 K)) = ((1 atm) (0.140 L) )/(x K)`

Now, we just need to solve for the unknown. Start by simplifying the left side and right numerator.

0.001 =
`(0.140 L)/(x K)`

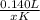
Multiply both sides by x.

0.001x = 0.140

Divide both sides by 0.001.

x = 140 K

Convert that to Celsius (K = C + 273)

140 = C + 273

C = -133

So, the volume of your gas will be 0.140 L at -133° C.