Answer: (x + 2)(3x - 2)(2x + 1)
Explanation:
First, find the possible rational roots. Then use synthetic division (or long division) to find a root. Next, factor the reduced polynomial.
6x³ + 11x² - 4x - 4
P = 4: ± 1, 2, 4
Q = 6: ± 1, 2, 3
Possible rational roots are: ± {1, 2, 4,
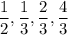 }
}
Try x = -2 --> which is the factor (x + 2)
-2 | 6 11 -4 -4
| ↓ -12 2 4
6 -1 -2 0 ← Remainder of 0 means (x + 2) is a factor
The reduced polynomial is:
6x² - 1x - 2
Factors of (6)(-2) = -12
∧
1 -12 = -11
2 -6 = -4
3 -4 = -1 this works!
Replace -1x with +3x - 4x and use the grouping method to factor:
6x² + 3x -4x -2
3x(2x + 1) -2(2x + 1) So the factors are: (3x - 2) and (2x + 1)