To answer this question, you need to find the solutions to the expression. The best way to find the solutions to this equation is to simplify it, or in other words to factor it down as much as you can.
If you look at both of the terms, you'll notice that 25 can be simplified to 5^2 and 81 can be simplified to 9^2.
So we can split the binomial into two seperate binomials.

Now, all we have to do is solve each part seperately. For time sake, I'm going to solve both of them at the same time.
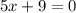

First, I'm going to add/subtract 9 for both of them to get rid of the +-9.
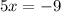
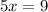
Then I will divide by 5 on both sides for both expressions. Notice how the answer is the same number for both of them, the only difference is one is negative and the other is positive.
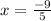
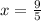
When you add a number to the negative version of itself, you end up with 0. For Ex.
-4 + 4 = 0
7 + (-7) = 0
So we can conclude that the sum of the two solutions above are equal to zero.