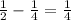Which number should follow in this series: 64/64 9/12 6/12

Question

asked Sep 2, 2020 35.8k views

2 Answers

Philantrovert · Answer 1 · 2020-09-05T13:24:38+0000

Answer:

$\texttt{The number following is }(1)/(4)$

Explanation:

Series is

(64)/(64),(9)/(12),(6)/(12).....

Let us simplify

(64)/(64),(9)/(12),(6)/(12).....=1,(3)/(4),(1)/(2).....

So this is arithmetic progression with 1 as first term and
-(1)/(4) as common difference.

Next term of AP will be
(1)/(2)-(1)/(4)=(1)/(4)

$\texttt{The number following is }(1)/(4)$

Sukhjeevan · Answer 2 · 2020-09-09T17:48:40+0000

Answer:

Explanation:

You can reduce the fractions, then:

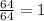
(64)/(64)=1

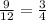
(9)/(12)=(3)/(4)

(6)/(12)=(3)/(6)=(1)/(2)

Rewrite them as following:

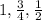
1,(3)/(4),(1)/(2)

If you subtract the first number and the second number, you obtain:

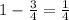
1-(3)/(4)=(1)/(4)

If you subtract the second number and the second number, you obtain:

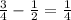
(3)/(4)-(1)/(2)=(1)/(4)

Therefore, you must subtract
(1)/(2) and
(1)/(4) to obtain the number asked. Then, this is:

(1)/(2)-(1)/(4)=(1)/(4)