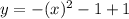Question

Please match each function formula with the corresponding transformation of the parent function y= -x^2-1

Answer 1

The answer in the attached figure

Explanation:

we have the parent function

`y=-x^(2)-1`

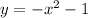
case 1) Reflected across the x-axis

we know that

The rule of the transformation is

(x,y)------> (x,-y)

so

`y=-(-x^(2)-1)`

`y=x^(2)+1`

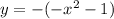
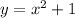
case 2) Reflected across the y-axis

we know that

The rule of the transformation is

(x,y)------> (-x,y)

so

`y=-(-x)^(2)-1`

`y=-x^(2)-1`

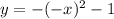
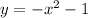
case 3) Translated left by 1 unit

we know that

The rule of the transformation is

(x,y)------> (x-1,y)

so

`y=-(x+1)^(2)-1`

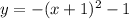
case 4) Translated right by 1 unit

we know that

The rule of the transformation is

(x,y)------> (x+1,y)

so

`y=-(x-1)^(2)-1`

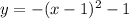
case 5) Translated down by 1 unit

we know that

The rule of the transformation is

(x,y)------> (x,y-1)

so

`y=-(x)^(2)-1-1`

`y=-(x)^(2)-2`

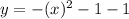
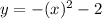
case 6) Translated up by 1 unit

we know that

The rule of the transformation is

(x,y)------> (x,y+1)

so

`y=-(x)^(2)-1+1`

`y=-(x)^(2)`