Question

What is the number of cycles of y=9cos(θ/4+3π/2)+4 between 0 and 2π?

Answer 1

Answer: Choice C) 1/4

===================================================

Work Shown:

Let's rearrange terms a bit to say the following:

`y = 9\cos\left((\theta)/(4)+(3\pi)/(2)\right)+4\\\\y = 9\cos\left((1)/(4)\theta+(3\pi)/(2)\right)+4\\\\y = 9\cos\left((1)/(4)\left(\theta+6\pi\right)\right)+4\\\\y = 9\cos\left((1)/(4)\left(\theta-(-6\pi)\right)\right)+4\\\\`

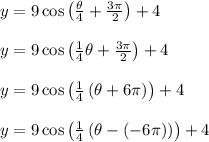
The last equation is in the form
`y = A\cos\left(B\left(\theta-C\right)\right)+D\\\\`

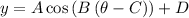
where,

• |A| = amplitude
• B handles the period. Specifically T = 2pi/B, where T is the period
• C handles the phase shift, aka horizontal shifting
• D determines the midline and the vertical shifting

We only need to worry about the value of B.

In this case, B = 1/4

So,

`T = (2\pi)/(B)\\\\T = 2\pi / B\\\\T = 2\pi / (1)/(4)\\\\T = 2\pi * (4)/(1)\\\\T = 8\pi\\\\`

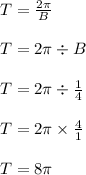
The period is 8pi. Every 8pi units, a full cycle is completed.

However, we're not going from 0 to 8pi, but instead from 0 to 2pi.

The given interval is 2pi units wide. This is (2pi)/(8pi) = 1/4 of a full cycle. This is why choice C is the answer.